Pro výpočet koule nepoužívám příkaz gluSphere(), ale napsal jsem algoritmus pro výpočet všech bodů.
Příklad zobrazí kouli v bodech příkazem glBegin(GL_Points), v čarách příkazem glBegin(GL_Lines) , nebo v trojúhleníkách
příkazem glBegin(GL_Triangles). Dále příklad obsahuje algoritmus pro výpočet normálových vektorů, aby včechny plochy koule byly
správně vystínovaný. Další algoritmus je pro výpočet texturové koordinace, aby se textura roztáhla rovnoměrně po celé kouli.
Nejdříve nadefinuju typy a proměnné
//Sphere
type TPoint3=record
x: double;
y: double;
z: double;
end;
type TPoint2=record
x: double;
y: double;
end;
type TVector=record
x: double;
y: double;
z: double;
end;
procedure CalcNormalVector(Vect1,Vect2,Vect3:TPoint3);
var
SpFace: integer=20; //Počet ploch koule
SpRadius: double=20; //Poloměr koule
SphereRot: double; //Rotace koule
SpPoint, //Body koule
SpNormal1, //Normálové vektory
SpNormal2,
SpNormal3,
SpNormal4: array [0..50, 0..100] of TPoint3;
SpNormalSmooth: TPoint3; //Normálový vektor pro vyhlazení stínu
SpCoord1, //Texturová koordinace
SpCoord2,
SpCoord3,
SpCoord4: array [0..50, 0..100] of TPoint2;
SpherePoints: boolean=true; //Zapne vypne body
SphereLines: boolean; //Zapne vypne čáry
SphereTriangles: boolean; //Zapne vypne trojúhelníky
NormalVector:TVector; //Výsledný normálový vektor
Tohle je procedura na výpočet všech bodů koule.
procedure InitSphere; {Calculate Sphere Points}
var
rVert, rHoriz: array [0..100] of double;
Angle: double;
i,j: integer;
begin
Angle := 360 / SpFace;
for i := 1 to (SpFace div 2)-1 do begin
rVert[i] := cos((i*Angle)*(pi/180))* SpRadius;
rHoriz[i] := sin((i*Angle)*(pi/180))* SpRadius;
for j := 1 to SpFace do begin
SpPoint[i,j].x := cos((j*Angle)*(pi/180)) * rHoriz[i];
SpPoint[i,j].y := rVert[i];
SpPoint[i,j].z := -sin((j*Angle)*(pi/180)) * rHoriz[i];
//first point
SpPoint[0,j].x := 0;
SpPoint[0,j].y := SpRadius;
SpPoint[0,j].z := 0;
//last point
SpPoint[SpFace div 2,j].x := 0;
SpPoint[SpFace div 2,j].y := -SpRadius;
SpPoint[SpFace div 2,j].z := 0;
end;
end;
SphereTexCoord;
SphereNormals;
end;
Nejdříve vypočítám úhel mezi jednotlivými body
Angle := 360 / SpFace;
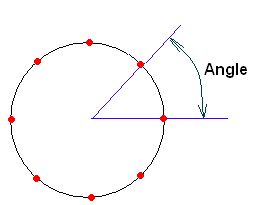
Cyklus
for i := 1 to (SpFace div 2)-1 do begin
definuje počet kružnic.
Cyklus
for j := 1 to SpFace do begin
definuje počet bodů v kružnici.
rVert[i] := cos((i*Angle)*(pi/180))* SpRadius;
vypočítá vzdálenost kružnice od prvního (horního) bodu koule.
rHoriz[i] := sin((i*Angle)*(pi/180))* SpRadius;
vypočítá poloměr kružnice.
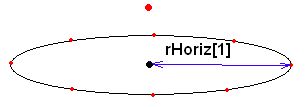
SpPoint[i,j].x := cos((j*Angle)*(pi/180)) * rHoriz[i];
SpPoint[i,j].y := rVert[i];
SpPoint[i,j].z := -sin((j*Angle)*(pi/180)) * rHoriz[i];
vypočítá souřadnice všech bodů v kružnici.
//first point
SpPoint[0,j].x := 0;
SpPoint[0,j].y := SpRadius;
SpPoint[0,j].z := 0;
//last point
SpPoint[SpFace div 2,j].x := 0;
SpPoint[SpFace div 2,j].y := -SpRadius;
SpPoint[SpFace div 2,j].z := 0;
vypočítá první (horní) a poslední (dolní) bod koule.
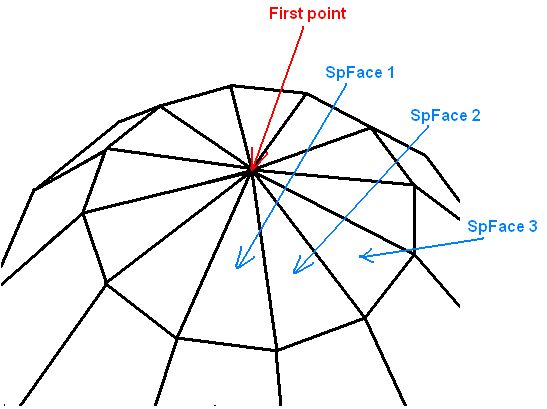
Teď, když mám vypočítaný všechny body koule, tak je použiju v proceduře DrawSphere, která mi
vyrenderuje kouli v bodech glBegin(GL_Points),
čarách glBegin(GL_Lines),
nebo trojúhelníkách glBegin(GL_Triangles).
procedure DrawSphere;
var
i,j: integer;
begin
glPushMatrix;
//Draw Points
if SpherePoints then begin
glDisable(GL_TEXTURE_2D);
glDisable(GL_LIGHTING);
glBegin(GL_Points);
for i := 1 to (SpFace div 2)-1 do begin
for j := 1 to SpFace do begin
glVertex3f(SpPoint[i,j].x,SpPoint[i,j].y,SpPoint[i,j].z);
end;
end;
glEnd;
glBegin(GL_Points);
glVertex3f(SpPoint[0,1].x,SpPoint[0,1].y,SpPoint[0,1].z);
glVertex3f(SpPoint[SpFace div 2,2].x,SpPoint[SpFace div 2,2].y,SpPoint[SpFace div 2,2].z);
glEnd;
glEnable(GL_LIGHTING);
end;
//Draw Lines
if SphereLines then begin
glDisable(GL_TEXTURE_2D);
glDisable(GL_LIGHTING);
glBegin(GL_Lines);
for i := 1 to (SpFace div 2)-1 do begin
for j := 1 to SpFace do begin
glVertex3f(SpPoint[i,j].x,SpPoint[i,j].y,SpPoint[i,j].z);
if j <> SpFace then
glVertex3f(SpPoint[i,j+1].x,SpPoint[i,j+1].y,SpPoint[i,j+1].z)
else
glVertex3f(SpPoint[i,1].x,SpPoint[i,1].y,SpPoint[i,1].z);
end;
end;
glEnd;
glBegin(GL_Lines);
for i := 1 to (SpFace div 2)-2 do begin
for j := 1 to SpFace do begin
glVertex3f(SpPoint[i,j].x,SpPoint[i,j].y,SpPoint[i,j].z);
glVertex3f(SpPoint[i+1,j].x,SpPoint[i+1,j].y,SpPoint[i+1,j].z)
end;
end;
glEnd;
//first point
glBegin(GL_Lines);
for j := 1 to SpFace do begin
glVertex3f(SpPoint[0,1].x,SpPoint[0,1].y,SpPoint[0,1].z);
glVertex3f(SpPoint[1,j].x,SpPoint[1,j].y,SpPoint[1,j].z)
end;
glEnd;
//last point
glBegin(GL_Lines);
for j := 1 to SpFace do begin
glVertex3f(SpPoint[SpFace div 2,2].x,SpPoint[SpFace div 2,2].y,SpPoint[SpFace div 2,2].z);
glVertex3f(SpPoint[(SpFace div 2)-1,j].x,SpPoint[(SpFace div 2)-1,j].y,SpPoint[(SpFace div 2)-1,j].z)
end;
glEnd;
glEnable(GL_LIGHTING);
end;
//Draw Triangles
if SphereTriangles then begin
glBindTexture(GL_TEXTURE_2D, TextureBin[1]);
glEnable(GL_TEXTURE_2D);
glBegin(GL_TRIANGLES);
for i := 1 to (SpFace div 2)-2 do begin
for j := 1 to SpFace do begin
if j <> SpFace then begin
glTexCoord2f(SpCoord1[i,j].x,SpCoord1[i,j].y);
glNormal3f(SpNormal1[i,j].x,SpNormal1[i,j].y,SpNormal1[i,j].z);
glVertex3f(SpPoint[i,j].x,SpPoint[i,j].y,SpPoint[i,j].z);
glTexCoord2f(SpCoord2[i,j+1].x,SpCoord2[i,j+1].y);
glNormal3f(SpNormal2[i,j+1].x,SpNormal2[i,j+1].y,SpNormal2[i,j+1].z);
glVertex3f(SpPoint[i,j+1].x,SpPoint[i,j+1].y,SpPoint[i,j+1].z);
glTexCoord2f(SpCoord3[i+1,j].x,SpCoord3[i+1,j].y);
glNormal3f(SpNormal3[i+1,j].x,SpNormal3[i+1,j].y,SpNormal3[i+1,j].z);
glVertex3f(SpPoint[i+1,j].x,SpPoint[i+1,j].y,SpPoint[i+1,j].z);
///////////////////////////////////////////////////////////////////
glTexCoord2f(SpCoord2[i,j+1].x,SpCoord2[i,j+1].y);
glNormal3f(SpNormal2[i,j+1].x,SpNormal2[i,j+1].y,SpNormal2[i,j+1].z);
glVertex3f(SpPoint[i,j+1].x,SpPoint[i,j+1].y,SpPoint[i,j+1].z);
glTexCoord2f(SpCoord3[i+1,j].x,SpCoord3[i+1,j].y);
glNormal3f(SpNormal3[i+1,j].x,SpNormal3[i+1,j].y,SpNormal3[i+1,j].z);
glVertex3f(SpPoint[i+1,j].x,SpPoint[i+1,j].y,SpPoint[i+1,j].z);
glTexCoord2f(SpCoord4[i+1,j+1].x,SpCoord4[i+1,j+1].y);
glNormal3f(SpNormal4[i+1,j+1].x,SpNormal4[i+1,j+1].y,SpNormal4[i+1,j+1].z);
glVertex3f(SpPoint[i+1,j+1].x,SpPoint[i+1,j+1].y,SpPoint[i+1,j+1].z);
end else begin
glTexCoord2f(SpCoord1[i,j].x,SpCoord1[i,j].y);
glNormal3f(SpNormal1[i,j].x,SpNormal1[i,j].y,SpNormal1[i,j].z);
glVertex3f(SpPoint[i,j].x,SpPoint[i,j].y,SpPoint[i,j].z);
glTexCoord2f(SpCoord2[i,1].x,SpCoord2[i,1].y);
glNormal3f(SpNormal2[i,1].x,SpNormal2[i,1].y,SpNormal2[i,1].z);
glVertex3f(SpPoint[i,1].x,SpPoint[i,1].y,SpPoint[i,1].z);
glTexCoord2f(SpCoord3[i+1,j].x,SpCoord3[i+1,j].y);
glNormal3f(SpNormal3[i+1,j].x,SpNormal3[i+1,j].y,SpNormal3[i+1,j].z);
glVertex3f(SpPoint[i+1,j].x,SpPoint[i+1,j].y,SpPoint[i+1,j].z);
///////////////////////////////////////////////////////////////////
glTexCoord2f(SpCoord2[i,1].x,SpCoord2[i,1].y);
glNormal3f(SpNormal2[i,1].x,SpNormal2[i,1].y,SpNormal2[i,1].z);
glVertex3f(SpPoint[i,1].x,SpPoint[i,1].y,SpPoint[i,1].z);
glTexCoord2f(SpCoord3[i+1,j].x,SpCoord3[i+1,j].y);
glNormal3f(SpNormal3[i+1,j].x,SpNormal3[i+1,j].y,SpNormal3[i+1,j].z);
glVertex3f(SpPoint[i+1,j].x,SpPoint[i+1,j].y,SpPoint[i+1,j].z);
glTexCoord2f(SpCoord4[i+1,1].x,SpCoord4[i+1,1].y);
glNormal3f(SpNormal4[i+1,1].x,SpNormal4[i+1,1].y,SpNormal4[i+1,1].z);
glVertex3f(SpPoint[i+1,1].x,SpPoint[i+1,1].y,SpPoint[i+1,1].z);
end;
end;
end;
glEnd;
//first point
glBegin(GL_TRIANGLES);
for j := 1 to SpFace do begin
glTexCoord2f(SpCoord1[0,j].x,SpCoord1[0,j].y);
glNormal3f(SpNormal1[0,j].x,SpNormal1[0,j].y,SpNormal1[0,j].z);
glVertex3f(SpPoint[0,j].x,SpPoint[0,j].y,SpPoint[0,j].z);
glTexCoord2f(SpCoord3[1,j].x,SpCoord3[1,j].y);
glNormal3f(SpNormal3[1,j].x,SpNormal3[1,j].y,SpNormal3[1,j].z);
glVertex3f(SpPoint[1,j].x,SpPoint[1,j].y,SpPoint[1,j].z);
if j <> SpFace then begin
glTexCoord2f(SpCoord4[1,j+1].x,SpCoord4[1,j+1].y);
glNormal3f(SpNormal4[1,j+1].x,SpNormal4[1,j+1].y,SpNormal4[1,j+1].z);
glVertex3f(SpPoint[1,j+1].x,SpPoint[1,j+1].y,SpPoint[1,j+1].z);
end else begin
glTexCoord2f(SpCoord4[1,1].x,SpCoord4[1,1].y);
glNormal3f(SpNormal4[1,1].x,SpNormal4[1,1].y,SpNormal4[1,1].z);
glVertex3f(SpPoint[1,1].x,SpPoint[1,1].y,SpPoint[1,1].z);
end;
end;
glEnd;
//last point
glBegin(GL_TRIANGLES);
for j := 1 to SpFace do begin
glTexCoord2f(SpCoord3[(SpFace div 2)+1,j].x,SpCoord3[(SpFace div 2)+1,j].y);
glNormal3f(SpNormal3[(SpFace div 2),j].x,SpNormal3[(SpFace div 2),j].y,SpNormal3[(SpFace div 2),j].z);
glVertex3f(SpPoint[(SpFace div 2),j].x,SpPoint[(SpFace div 2),j].y,SpPoint[(SpFace div 2),j].z);
glTexCoord2f(SpCoord1[(SpFace div 2),j].x,SpCoord1[(SpFace div 2),j].y);
glNormal3f(SpNormal1[(SpFace div 2)-1,j].x,SpNormal1[(SpFace div 2)-1,j].y,SpNormal1[(SpFace div 2)-1,j].z);
glVertex3f(SpPoint[(SpFace div 2)-1,j].x,SpPoint[(SpFace div 2)-1,j].y,SpPoint[(SpFace div 2)-1,j].z);
if j <> SpFace then begin
glTexCoord2f(SpCoord2[(SpFace div 2),j+1].x,SpCoord2[(SpFace div 2),j+1].y);
glNormal3f(SpNormal2[(SpFace div 2)-1,j+1].x,SpNormal2[(SpFace div 2)-1,j+1].y,SpNormal2[(SpFace div 2)-1,j+1].z);
glVertex3f(SpPoint[(SpFace div 2)-1,j+1].x,SpPoint[(SpFace div 2)-1,j+1].y,SpPoint[(SpFace div 2)-1,j+1].z);
end else begin
glTexCoord2f(SpCoord2[(SpFace div 2),1].x,SpCoord2[(SpFace div 2),1].y);
glNormal3f(SpNormal2[(SpFace div 2)-1,1].x,SpNormal2[(SpFace div 2)-1,1].y,SpNormal2[(SpFace div 2)-1,1].z);
glVertex3f(SpPoint[(SpFace div 2)-1,1].x,SpPoint[(SpFace div 2)-1,1].y,SpPoint[(SpFace div 2)-1,1].z);
end;
end;
glEnd;
end;
glPopMatrix;
end;
Aby trojúhelníky byly správně vystínovaný, musí se vypočítat jejich normálové vektory.
procedure CalcNormalVector(Vect1,Vect2,Vect3:TPoint3);
var longi,vx1,vy1,vz1,vx2,vy2,vz2:double;
VectRes:TVector;
begin
vx1:=Vect1.x-Vect2.x;vy1:=Vect1.y-Vect2.y;vz1:=Vect1.z-Vect2.z;
vx2:=Vect2.x-Vect3.x;vy2:=Vect2.y-Vect3.y;vz2:=Vect2.z-Vect3.z;
with VectRes do begin
x:=vy1*vz2 - vz1*vy2;
y:=vz1*vx2 - vx1*vz2;
z:=vx1*vy2 - vy1*vx2;
//Optimalization vector
longi:=sqrt(sqr (x) + sqr(y) + sqr(z));
if longi>0 then //avoid zero division error
x:=x/longi;y:=y/longi;z:=z/longi;
end;
NormalVector := VectRes;
end;
Předchozí procedura CalcNormalVector vypočítá normálový vektor ze tří
vstupních bodů Vect1,Vect2,Vect3.
Následující procedura SphereNormals vybere
správné tři vstupní body a pošle proceduře CalcNormalVector. Výsledné hodnoty
uloží do normálových vektorů SpNormal1, SpNormal2, SpNormal3, SpNormal4, které se používají v
proceduře DrawSphere.
procedure SphereNormals;
var
Vect1, Vect2, Vect3, Vect4: TPoint3;
i,j: integer;
begin
for i := 1 to (SpFace div 2)-2 do begin
for j := 1 to SpFace do begin
if j <> SpFace then begin
Vect1.x := SpPoint[i,j].x;
Vect1.y := SpPoint[i,j].y;
Vect1.z := SpPoint[i,j].z;
Vect2.x := SpPoint[i,j+1].x;
Vect2.y := SpPoint[i,j+1].y;
Vect2.z := SpPoint[i,j+1].z;
Vect3.x := SpPoint[i+1,j].x;
Vect3.y := SpPoint[i+1,j].y;
Vect3.z := SpPoint[i+1,j].z;
Vect4.x := SpPoint[i+1,j+1].x;
Vect4.y := SpPoint[i+1,j+1].y;
Vect4.z := SpPoint[i+1,j+1].z;
// Vertex Normal Point 1
CalcNormalVector(Vect1,Vect3,Vect2);
SpNormal1[i,j].x := NormalVector.x;
SpNormal1[i,j].y := NormalVector.y;
SpNormal1[i,j].z := NormalVector.z;
// Vertex Normal Point 2
CalcNormalVector(Vect2,Vect3,Vect4);
SpNormal2[i,j+1].x := NormalVector.x;
SpNormal2[i,j+1].y := NormalVector.y;
SpNormal2[i,j+1].z := NormalVector.z;
// Vertex Normal Point 3
CalcNormalVector(Vect3,Vect2,Vect1);
SpNormal3[i+1,j].x := NormalVector.x;
SpNormal3[i+1,j].y := NormalVector.y;
SpNormal3[i+1,j].z := NormalVector.z;
// Vertex Normal Point 4
CalcNormalVector(Vect4,Vect2,Vect3);
SpNormal4[i+1,j+1].x := NormalVector.x;
SpNormal4[i+1,j+1].y := NormalVector.y;
SpNormal4[i+1,j+1].z := NormalVector.z;
end else begin
Vect1.x := SpPoint[i,j].x;
Vect1.y := SpPoint[i,j].y;
Vect1.z := SpPoint[i,j].z;
Vect2.x := SpPoint[i,1].x;
Vect2.y := SpPoint[i,1].y;
Vect2.z := SpPoint[i,1].z;
Vect3.x := SpPoint[i+1,j].x;
Vect3.y := SpPoint[i+1,j].y;
Vect3.z := SpPoint[i+1,j].z;
Vect4.x := SpPoint[i+1,1].x;
Vect4.y := SpPoint[i+1,1].y;
Vect4.z := SpPoint[i+1,1].z;
// Vertex Normal Point 1
CalcNormalVector(Vect1,Vect3,Vect2);
SpNormal1[i,j].x := NormalVector.x;
SpNormal1[i,j].y := NormalVector.y;
SpNormal1[i,j].z := NormalVector.z;
// Vertex Normal Point 2
CalcNormalVector(Vect2,Vect3,Vect4);
SpNormal2[i,1].x := NormalVector.x;
SpNormal2[i,1].y := NormalVector.y;
SpNormal2[i,1].z := NormalVector.z;
// Vertex Normal Point 3
CalcNormalVector(Vect3,Vect2,Vect1);
SpNormal3[i+1,j].x := NormalVector.x;
SpNormal3[i+1,j].y := NormalVector.y;
SpNormal3[i+1,j].z := NormalVector.z;
// Vertex Normal Point 4
CalcNormalVector(Vect4,Vect2,Vect3);
SpNormal4[i+1,1].x := NormalVector.x;
SpNormal4[i+1,1].y := NormalVector.y;
SpNormal4[i+1,1].z := NormalVector.z;
end;
end;
end;
//first point
for j := 1 to SpFace do begin
if j <> SpFace then begin
Vect1.x := SpPoint[0,j].x;
Vect1.y := SpPoint[0,j].y;
Vect1.z := SpPoint[0,j].z;
Vect2.x := SpPoint[1,j].x;
Vect2.y := SpPoint[1,j].y;
Vect2.z := SpPoint[1,j].z;
Vect3.x := SpPoint[1,j+1].x;
Vect3.y := SpPoint[1,j+1].y;
Vect3.z := SpPoint[1,j+1].z;
// Vertex Normal Point 1
CalcNormalVector(Vect1,Vect2,Vect3);
SpNormal1[0,j].x := NormalVector.x;
SpNormal1[0,j].y := NormalVector.y;
SpNormal1[0,j].z := NormalVector.z;
// Vertex Normal Point 2
CalcNormalVector(Vect2,Vect3,Vect1);
SpNormal3[1,j].x := NormalVector.x;
SpNormal3[1,j].y := NormalVector.y;
SpNormal3[1,j].z := NormalVector.z;
// Vertex Normal Point 3
CalcNormalVector(Vect3,Vect1,Vect2);
SpNormal4[1,j+1].x := NormalVector.x;
SpNormal4[1,j+1].y := NormalVector.y;
SpNormal4[1,j+1].z := NormalVector.z;
end else begin
Vect1.x := SpPoint[0,j].x;
Vect1.y := SpPoint[0,j].y;
Vect1.z := SpPoint[0,j].z;
Vect2.x := SpPoint[1,j].x;
Vect2.y := SpPoint[1,j].y;
Vect2.z := SpPoint[1,j].z;
Vect3.x := SpPoint[1,1].x;
Vect3.y := SpPoint[1,1].y;
Vect3.z := SpPoint[1,1].z;
// Vertex Normal Point 1
CalcNormalVector(Vect1,Vect2,Vect3);
SpNormal1[0,j].x := NormalVector.x;
SpNormal1[0,j].y := NormalVector.y;
SpNormal1[0,j].z := NormalVector.z;
// Vertex Normal Point 2
CalcNormalVector(Vect2,Vect3,Vect1);
SpNormal3[1,j].x := NormalVector.x;
SpNormal3[1,j].y := NormalVector.y;
SpNormal3[1,j].z := NormalVector.z;
// Vertex Normal Point 3
CalcNormalVector(Vect3,Vect1,Vect2);
SpNormal4[1,1].x := NormalVector.x;
SpNormal4[1,1].y := NormalVector.y;
SpNormal4[1,1].z := NormalVector.z;
end;
end;
//last point
for j := 1 to SpFace do begin
if j <> SpFace then begin
Vect1.x := SpPoint[(SpFace div 2)-1,j].x;
Vect1.y := SpPoint[(SpFace div 2)-1,j].y;
Vect1.z := SpPoint[(SpFace div 2)-1,j].z;
Vect2.x := SpPoint[(SpFace div 2)-1,j+1].x;
Vect2.y := SpPoint[(SpFace div 2)-1,j+1].y;
Vect2.z := SpPoint[(SpFace div 2)-1,j+1].z;
Vect3.x := SpPoint[(SpFace div 2),j].x;
Vect3.y := SpPoint[(SpFace div 2),j].y;
Vect3.z := SpPoint[(SpFace div 2),j].z;
// Vertex Normal Point 1
CalcNormalVector(Vect1,Vect3,Vect2);
SpNormal1[(SpFace div 2)-1,j].x := NormalVector.x;
SpNormal1[(SpFace div 2)-1,j].y := NormalVector.y;
SpNormal1[(SpFace div 2)-1,j].z := NormalVector.z;
// Vertex Normal Point 2
CalcNormalVector(Vect2,Vect1,Vect3);
SpNormal2[(SpFace div 2)-1,j+1].x := NormalVector.x;
SpNormal2[(SpFace div 2)-1,j+1].y := NormalVector.y;
SpNormal2[(SpFace div 2)-1,j+1].z := NormalVector.z;
// Vertex Normal Point 3
CalcNormalVector(Vect3,Vect2,Vect1);
SpNormal3[(SpFace div 2),j].x := NormalVector.x;
SpNormal3[(SpFace div 2),j].y := NormalVector.y;
SpNormal3[(SpFace div 2),j].z := NormalVector.z;
end else begin
Vect1.x := SpPoint[(SpFace div 2)-1,j].x;
Vect1.y := SpPoint[(SpFace div 2)-1,j].y;
Vect1.z := SpPoint[(SpFace div 2)-1,j].z;
Vect2.x := SpPoint[(SpFace div 2)-1,1].x;
Vect2.y := SpPoint[(SpFace div 2)-1,1].y;
Vect2.z := SpPoint[(SpFace div 2)-1,1].z;
Vect3.x := SpPoint[(SpFace div 2),j].x;
Vect3.y := SpPoint[(SpFace div 2),j].y;
Vect3.z := SpPoint[(SpFace div 2),j].z;
// Vertex Normal Point 1
CalcNormalVector(Vect1,Vect3,Vect2);
SpNormal1[(SpFace div 2)-1,j].x := NormalVector.x;
SpNormal1[(SpFace div 2)-1,j].y := NormalVector.y;
SpNormal1[(SpFace div 2)-1,j].z := NormalVector.z;
// Vertex Normal Point 2
CalcNormalVector(Vect2,Vect1,Vect3);
SpNormal2[(SpFace div 2)-1,1].x := NormalVector.x;
SpNormal2[(SpFace div 2)-1,1].y := NormalVector.y;
SpNormal2[(SpFace div 2)-1,1].z := NormalVector.z;
// Vertex Normal Point 3
CalcNormalVector(Vect3,Vect2,Vect1);
SpNormal3[(SpFace div 2),j].x := NormalVector.x;
SpNormal3[(SpFace div 2),j].y := NormalVector.y;
SpNormal3[(SpFace div 2),j].z := NormalVector.z;
end;
end;
end;
Předchozí procedura SphereNormalsvypočítá normálové vektory všech plošek koule.
Všechny plošky jsou však ostře ohraničeny a koule je kostrbatá.
Proto jsem napsal proceduru SphereSmoothNormals která stíny vyhladí.
procedure SphereSmoothNormals;
var
i,j: integer;
SpNormalXpom, SpNormalYpom, SpNormalZpom: double;
begin
for i := 1 to (SpFace div 2)-1 do begin
for j := 1 to SpFace do begin
SpNormalSmooth.x := (SpNormal1[i,j].x + SpNormal2[i,j].x + SpNormal3[i,j].x + SpNormal4[i,j].x)/4;
SpNormalSmooth.y := (SpNormal1[i,j].y + SpNormal2[i,j].y + SpNormal3[i,j].y + SpNormal4[i,j].y)/4;
SpNormalSmooth.z := (SpNormal1[i,j].z + SpNormal2[i,j].z + SpNormal3[i,j].z + SpNormal4[i,j].z)/4;
SpNormal1[i,j].x := SpNormalSmooth.x;
SpNormal1[i,j].y := SpNormalSmooth.y;
SpNormal1[i,j].z := SpNormalSmooth.z;
SpNormal2[i,j].x := SpNormalSmooth.x;
SpNormal2[i,j].y := SpNormalSmooth.y;
SpNormal2[i,j].z := SpNormalSmooth.z;
SpNormal3[i,j].x := SpNormalSmooth.x;
SpNormal3[i,j].y := SpNormalSmooth.y;
SpNormal3[i,j].z := SpNormalSmooth.z;
SpNormal4[i,j].x := SpNormalSmooth.x;
SpNormal4[i,j].y := SpNormalSmooth.y;
SpNormal4[i,j].z := SpNormalSmooth.z;
end;
end;
//first point
for j := 1 to SpFace do begin
SpNormalXpom := SpNormalXpom + SpNormal1[0,j].x;
SpNormalYpom := SpNormalYpom + SpNormal1[0,j].y;
SpNormalZpom := SpNormalZpom + SpNormal1[0,j].z;
end;
for j := 1 to SpFace do begin
SpNormal1[0,j].x := SpNormalXpom / SpFace;
SpNormal1[0,j].y := SpNormalYpom / SpFace;
SpNormal1[0,j].z := SpNormalZpom / SpFace;
end;
//last point
SpNormalXpom := 0;
SpNormalYpom := 0;
SpNormalZpom := 0;
for j := 1 to SpFace do begin
SpNormalXpom := SpNormalXpom + SpNormal3[(SpFace div 2),j].x;
SpNormalYpom := SpNormalYpom + SpNormal3[(SpFace div 2),j].y;
SpNormalZpom := SpNormalZpom + SpNormal3[(SpFace div 2),j].z;
end;
for j := 1 to SpFace do begin
SpNormal3[(SpFace div 2),j].x := SpNormalXpom / SpFace;
SpNormal3[(SpFace div 2),j].y := SpNormalYpom / SpFace;
SpNormal3[(SpFace div 2),j].z := SpNormalZpom / SpFace;
end;
end;
Normálový vektor pro vyhlazení stínu vypočítám tak, že sečtu normálové vektory okolních ploch a vydělím počtem ploch.
for i := 1 to (SpFace div 2)-1 do begin
for j := 1 to SpFace do begin
SpNormalSmooth.x := (SpNormal1[i,j].x + SpNormal2[i,j].x + SpNormal3[i,j].x + SpNormal4[i,j].x)/4;
SpNormalSmooth.y := (SpNormal1[i,j].y + SpNormal2[i,j].y + SpNormal3[i,j].y + SpNormal4[i,j].y)/4;
SpNormalSmooth.z := (SpNormal1[i,j].z + SpNormal2[i,j].z + SpNormal3[i,j].z + SpNormal4[i,j].z)/4;
SpNormal1[i,j].x := SpNormalSmooth.x;
SpNormal1[i,j].y := SpNormalSmooth.y;
SpNormal1[i,j].z := SpNormalSmooth.z;
SpNormal2[i,j].x := SpNormalSmooth.x;
SpNormal2[i,j].y := SpNormalSmooth.y;
SpNormal2[i,j].z := SpNormalSmooth.z;
SpNormal3[i,j].x := SpNormalSmooth.x;
SpNormal3[i,j].y := SpNormalSmooth.y;
SpNormal3[i,j].z := SpNormalSmooth.z;
SpNormal4[i,j].x := SpNormalSmooth.x;
SpNormal4[i,j].y := SpNormalSmooth.y;
SpNormal4[i,j].z := SpNormalSmooth.z;
end;
end;
První a poslední bod koule počítám trochu jinak, protože okolních ploch je tolik, kolik je zadaných SpFace.
//first point
for j := 1 to SpFace do begin
SpNormalXpom := SpNormalXpom + SpNormal1[0,j].x;
SpNormalYpom := SpNormalYpom + SpNormal1[0,j].y;
SpNormalZpom := SpNormalZpom + SpNormal1[0,j].z;
end;
for j := 1 to SpFace do begin
SpNormal1[0,j].x := SpNormalXpom / SpFace;
SpNormal1[0,j].y := SpNormalYpom / SpFace;
SpNormal1[0,j].z := SpNormalZpom / SpFace;
end;
//last point
SpNormalXpom := 0;
SpNormalYpom := 0;
SpNormalZpom := 0;
for j := 1 to SpFace do begin
SpNormalXpom := SpNormalXpom + SpNormal3[(SpFace div 2),j].x;
SpNormalYpom := SpNormalYpom + SpNormal3[(SpFace div 2),j].y;
SpNormalZpom := SpNormalZpom + SpNormal3[(SpFace div 2),j].z;
end;
for j := 1 to SpFace do begin
SpNormal3[(SpFace div 2),j].x := SpNormalXpom / SpFace;
SpNormal3[(SpFace div 2),j].y := SpNormalYpom / SpFace;
SpNormal3[(SpFace div 2),j].z := SpNormalZpom / SpFace;
end;
Nakonec jsem vypočítal texturové koordinace všech plošek.
procedure SphereTexCoord;
var
x,y: double;
i,j: integer;
begin
y := 1/((SpFace div 2));
x := 1/SpFace;
for i := 1 to (SpFace div 2)-2 do begin
for j := 1 to SpFace do begin
if j <> SpFace then begin
SpCoord1[i,j].x := (j-1) * x;
SpCoord1[i,j].y := (i) * y;
SpCoord2[i,j+1].x := j * x;
SpCoord2[i,j+1].y := (i) * y;
SpCoord3[i+1,j].x := (j-1) * x;
SpCoord3[i+1,j].y := (i+1) * y;
SpCoord4[i+1,j+1].x := j * x;
SpCoord4[i+1,j+1].y := (i+1) * y;
end else begin
SpCoord1[i,j].x := (j-1) * x;
SpCoord1[i,j].y := (i) * y;
SpCoord2[i,1].x := j * x;
SpCoord2[i,1].y := (i) * y;
SpCoord3[i+1,j].x := (j-1) * x;
SpCoord3[i+1,j].y := (i+1) * y;
SpCoord4[i+1,1].x := j * x;
SpCoord4[i+1,1].y := (i+1) * y;
end;
end;
end;
//first point
for j := 1 to SpFace do begin
if j <> SpFace then begin
SpCoord1[0,j].x := ((j-1)*x)+(x/2);
SpCoord1[0,j].y := 0;
SpCoord3[1,j].x := (j-1)*x;
SpCoord3[1,j].y := y;
SpCoord4[1,j+1].x := (j)*x;
SpCoord4[1,j+1].y := y;
end else begin
SpCoord1[0,j].x := ((j-1)*x)+(x/2);
SpCoord1[0,j].y := 0;
SpCoord3[1,j].x := (j-1)*x;
SpCoord3[1,j].y := y;
SpCoord4[1,1].x := (j)*x;
SpCoord4[1,1].y := y;
end;
end;
//last point
for j := 1 to SpFace do begin
if j <> SpFace then begin
SpCoord3[(SpFace div 2)+1,j].x := ((j-1)*x)+(x/2);
SpCoord3[(SpFace div 2)+1,j].y := 1;
SpCoord1[(SpFace div 2),j].x := (j-1)*x;
SpCoord1[(SpFace div 2),j].y := i*y;
SpCoord2[(SpFace div 2),j+1].x := (j)*x;
SpCoord2[(SpFace div 2),j+1].y := i*y;
end else begin
SpCoord3[(SpFace div 2)+1,j].x := ((j-1)*x)+(x/2);
SpCoord3[(SpFace div 2)+1,j].y := 1;
SpCoord1[(SpFace div 2),j].x := (j-1)*x;
SpCoord1[(SpFace div 2),j].y := i*y;
SpCoord2[(SpFace div 2),1].x := (j)*x;
SpCoord2[(SpFace div 2),1].y := i*y;
end;
end;
end;
y := 1/((SpFace div 2));
x := 1/SpFace;
Výpočet x,y souřadnice textury.
Výsledná hodnota se potom v každém cyklu přičítá.
for i := 1 to (SpFace div 2)-2 do begin
for j := 1 to SpFace do begin
if j <> SpFace then begin
SpCoord1[i,j].x := (j-1) * x;
SpCoord1[i,j].y := (i) * y;
SpCoord2[i,j+1].x := j * x;
SpCoord2[i,j+1].y := (i) * y;
SpCoord3[i+1,j].x := (j-1) * x;
SpCoord3[i+1,j].y := (i+1) * y;
SpCoord4[i+1,j+1].x := j * x;
SpCoord4[i+1,j+1].y := (i+1) * y;
end else begin
SpCoord1[i,j].x := (j-1) * x;
SpCoord1[i,j].y := (i) * y;
SpCoord2[i,1].x := j * x;
SpCoord2[i,1].y := (i) * y;
SpCoord3[i+1,j].x := (j-1) * x;
SpCoord3[i+1,j].y := (i+1) * y;
SpCoord4[i+1,1].x := j * x;
SpCoord4[i+1,1].y := (i+1) * y;
end;
end;
end;
//first point
for j := 1 to SpFace do begin
if j <> SpFace then begin
SpCoord1[0,j].x := ((j-1)*x)+(x/2);
SpCoord1[0,j].y := 0;
SpCoord3[1,j].x := (j-1)*x;
SpCoord3[1,j].y := y;
SpCoord4[1,j+1].x := (j)*x;
SpCoord4[1,j+1].y := y;
end else begin
SpCoord1[0,j].x := ((j-1)*x)+(x/2);
SpCoord1[0,j].y := 0;
SpCoord3[1,j].x := (j-1)*x;
SpCoord3[1,j].y := y;
SpCoord4[1,1].x := (j)*x;
SpCoord4[1,1].y := y;
end;
end;
//last point
for j := 1 to SpFace do begin
if j <> SpFace then begin
SpCoord3[(SpFace div 2)+1,j].x := ((j-1)*x)+(x/2);
SpCoord3[(SpFace div 2)+1,j].y := 1;
SpCoord1[(SpFace div 2),j].x := (j-1)*x;
SpCoord1[(SpFace div 2),j].y := i*y;
SpCoord2[(SpFace div 2),j+1].x := (j)*x;
SpCoord2[(SpFace div 2),j+1].y := i*y;
end else begin
SpCoord3[(SpFace div 2)+1,j].x := ((j-1)*x)+(x/2);
SpCoord3[(SpFace div 2)+1,j].y := 1;
SpCoord1[(SpFace div 2),j].x := (j-1)*x;
SpCoord1[(SpFace div 2),j].y := i*y;
SpCoord2[(SpFace div 2),1].x := (j)*x;
SpCoord2[(SpFace div 2),1].y := i*y;
end;
end;
Celé zdrojáky si můžete prohlídnout
Normal_f
ControlPanel_f
Home
